Witt group

For Witt group in the theory of algebraic groups, see Witt vector.

In mathematics, a Witt group of a field, named after Ernst Witt, is an abelian group whose elements are represented by symmetric bilinear forms over the field.

Contents

Definition

Fix a field k. All vector spaces will be assumed to be finite-dimensional. We say that two symmetric bilinear forms are equivalent if one can be obtained from the other by adding zero or more copies of a hyperbolic plane (the non-degenerate two-dimensional symmetric bilinear form with a norm 0 vector). The Witt group of k is the abelian group of equivalence classes of non-degenerate symmetric bilinear forms, with the group operation corresponding to the orthogonal direct sum of forms.

The Witt group of k can be given a commutative ring structure, by using the tensor product of two bilinear forms to define the ring product. This is sometimes called the Witt ring of k, though the term "Witt ring" is often also used for a completely different ring of Witt vectors.

Witt equivalence

Two fields are said to be Witt equivalent if their Witt rings are isomorphic. Two number fields K and L are Witt equivalent if and only if there is a bijection T between the places of K and the places of L and a group isomorphism t between their square-class groups, preserving degree 2 Hilbert symbols. In this case the pair (T,t) is called a reciprocity equivalence or a degree 2 Hilbert symbol equivalence. Some variations and extensions of this condition, such as "tame degree l Hilbert symbol equivalence", have also been studied; see the references for details.

Generalizations

Main article: L-theory

Witt groups can also be defined in the same way for skew-symmetric forms, and for quadratic forms, and more generally ε-quadratic forms, over any *-ring R.

The resulting groups (and generalizations thereof) are known as the even-dimensional symmetric L-groups 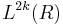L^{2k}(R) and even-dimensional quadratic L-groups 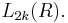L_{2k}(R). The quadratic L-groups are 4-periodic, with 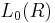L_0(R) being the Witt group of (1)-quadratic forms (symmetric), and 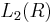L_2(R) being the Witt group of 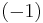(-1)-quadratic forms (skew-symmetric); symmetric L-groups are not 4-periodic for all rings, hence they provide a less exact generalization.

L-groups are central objects in surgery theory, forming one of the three terms of the surgery exact sequence.

References